Derivation of Bearing Rotation Frequencies

I recently had to work with bearings and their defects, and one of the concepts I had to get around was about the different frequencies involved with it. They are useful as knowing these frequencies often allow us to determine whether motors are broken just by looking at how they vibrate. That is a whole different issue altogether which I can also write about.

However, I found that while the frequencies are quite easy to understand, they are not that easy to derive. I found that there are a lack of good resources online for this derivation (according to my quick Google search). Therefore as a physicist who haven’t done mechanics in a while, I spent a day or so finding a derivation for the bearing frequencies and provided the proofs below. Enjoy.

But before we get to the derivations - a quick preliminary.

Preliminary - Rolling Without Slipping

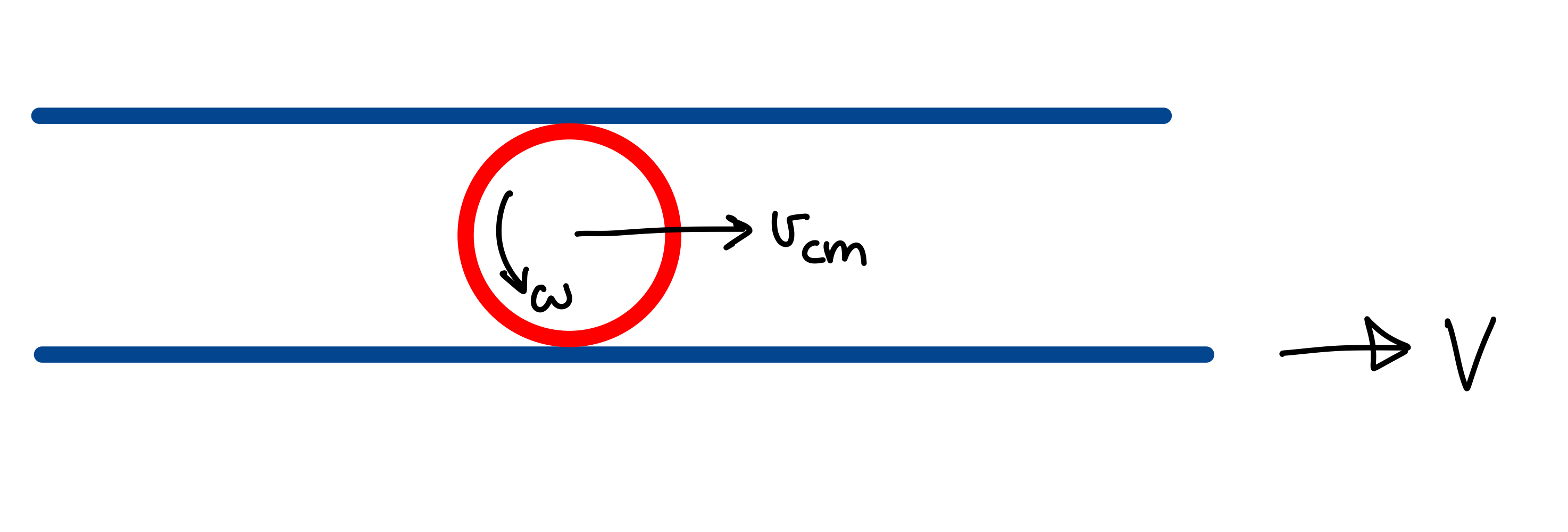
Rolling without slipping. Taken from a slide here.

Imagine just rolling the ball smoothly along the floor. In this case, the ball you have will be both rotating around its centre of mass with some angular velocity $\omega$, and is also moving forward at some speed $v_{CM}$. We can see that we can break these motions down separately.

The rotation motion will result in each part of the ball to move in a circle (as seen above in the circulating arrow). Some parts will be moving forward, while some will look like its going backwards. We can see though that this speed will be equal to $\omega r$ where $r$ is the distance from the centre of rotation to the particular point on the ball (for example, if we wanted the speed at the surface of the ball then $r$ would just be the radius of the ball).

At the same time, the translation motion will result in each part of the ball to move forward with the speed of $v_{CM}$, in the direction of the rolling.

The result of this is each part of the ball has its own speed. In many cases, we deal with instances where the ball is rolling without slipping, which means the bottom part of the ball is stationary with respect to the floor. For this to be the case, it must mean that $v_{CM} = \omega R$ where $R$ is the radius of the ball. Under this condition, the part of the ball touching the ground will have a speed of zero relative to the ground.

Ball rolling between two planes

Now, consider a slightly different scenario, where we now have a ball which is between two planes. Suppose the bottom plane is moving at some speed $V$ and the top plane is stationary (speed of zero). Assume the ball is rolling smoothly (i.e. no slipping) between the planes. Then, the speed of the part of the ball touching the bottom plane must have the speed $V$, and the speed of the part of the ball touching the top plane must have the speed of zero. From the diagram, we can write this as $v_{CM} + \omega R = V$, and $v_{CM} - \omega R = 0$. This solves to $v_{CM} = \frac{V}{2}$ and $\omega = \frac{V}{2R}$. We will use this fact later on.

The Bearing

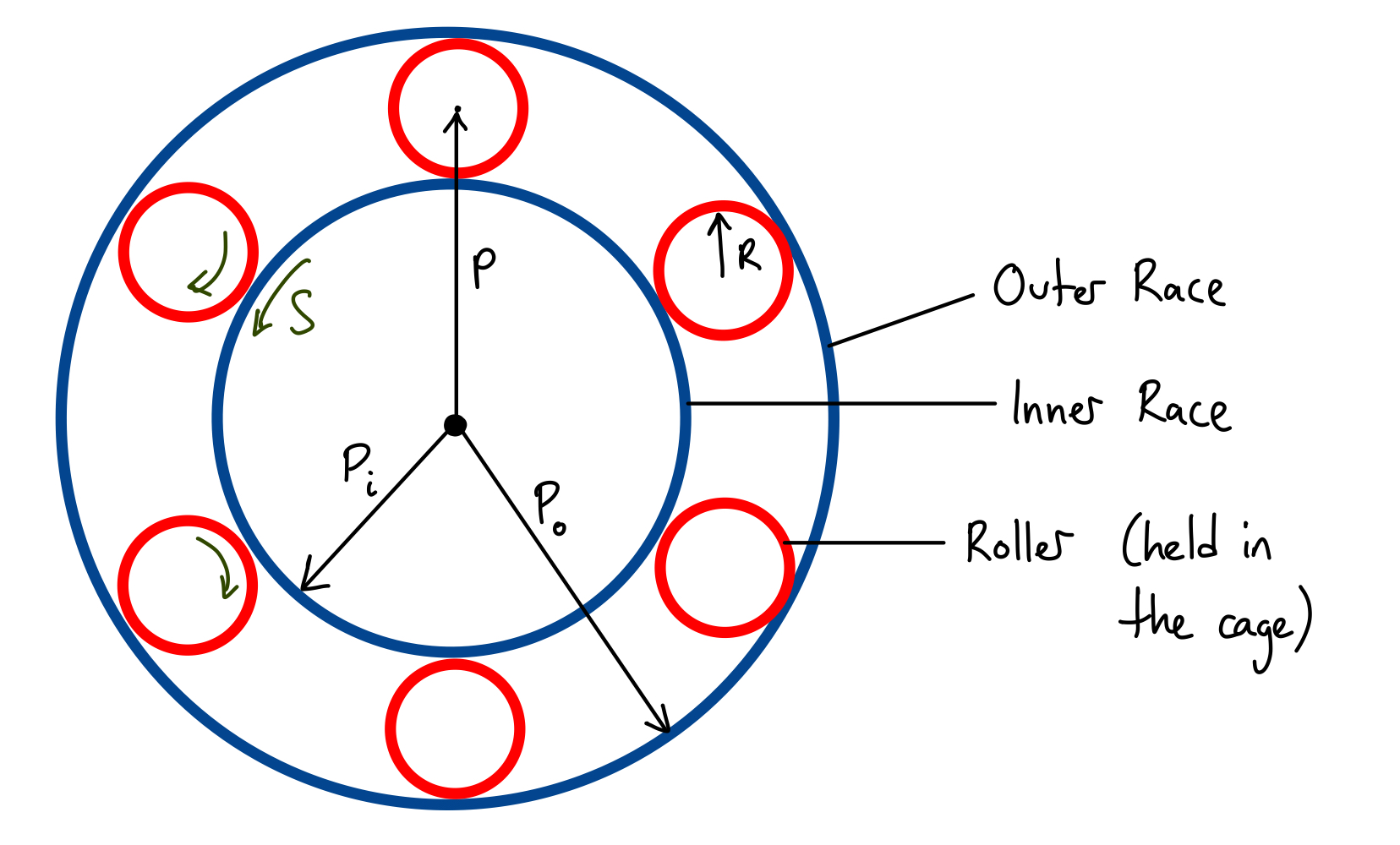
Consider the following setup of bearing. Here, we have the rollers (in red) which are rolling between the outer and inner race. For a more complete description of a bearing working, check out Wikipedia page on bearings or some other sources online.

In this case, we will be rotating the inner race (for example, having a shaft in the hole and rotating the shaft).

Cross-section of a simplified bearing

• $S$ is the revolution speed of the inner race (in revolutions per second)
• $N$ is the number of rollers (balls) the bearing has (for the image above, $N = 6$)
• $R$ is the radius of the roller
• $P$ is the radius of the cage (i.e. radius of the circular path of the rollers)
• $P_o$ is the radius of the outer race
• $P_i$ is the radius of the inner race

You might notice that the radii values are actually all related. We will address this later.

Relevant Speeds

Assume the outer ring is stationary. First of all, what is the speed of the inner ring? Since the inner ring is moving at the frequency of $S$, its angular speed is $2\pi S$. The inner ring has a radius of $P_i$, so the speed of the ring rotation is $2\pi S P_i$.

Now, we can view the bearing as rollers between two planes (in this case, the two races). Previously we have considered the planes to be flat, but here, the maths will work out the same. We can then assume that the rollers are now moving between two planes, where one plane (the inner race) moves at the speed of $2\pi S R_i$, and other plane (the outer race) is stationary. From above, we can then see that the rollers must be moving at a velocity of $v_{CM} = \frac{2\pi S P_i}{2} = \pi S P_i$, and the rollers are rotating at the speed of $\omega = \frac{2\pi S P_i}{2R} = \frac{\pi S P_i}{R}$.

Frequency Derivations

Fundamental Train Frequency (FTF)

This is the frequency of the rotation of the cage, i.e. how often the cage makes a complete revolution around the bearing. Note that the cage is what spaces the rollers apart, so it will actually move at the same speed as the rollers. To find the $FTF$, we just have to find the frequency of the rollers revolving around the bearing.

The rollers are moving at speed of $v_{CM}$, and it moves with this same speed throughout (note that the velocity is not the same). To complete one revolution, the roller must move a distance of one loop, which is equal to a distance (not displacement) of $2\pi P$. Here, we can easily see that it takes the roller a time of $\frac{2\pi P}{v_{CM}}$ to move around the bearing once.

This means that the frequency of the roller making a revolution around the bearing (i.e. the $FTF$) is the reciprocal of this. We can therefore see that

Ball Pass Frequency Outer (BPFO)

This is the frequency that a roller passes a certain point on the outer race. You can think of having a little mark on the outer race, and try to observe how frequently the rollers will pass through that mark. This is the $BPFO$.

This value is actually quite straightforward to compute. First, assume that you have a single roller. The roller will revolve around the bearing with a frequency equal to the $FTF$, and so the frequency that the one ball will revolve through the outer race will also be equal to $FTF$.

Instead, if we now have $N$ rollers, then we can see that for any point on the outer race, the rollers will pass through that point $N$ times more frequently since there are $N$ rollers revolving around the bearing. We can therefore see that

Ball Pass Frequency Inner (BPFI)

Bearing motion in frame with stationary outer race (left) and stationary inner race (left)

Similar to the $BPFO$, this is the frequency that a roller passes a certain point on the inner race. By similar logic one might think that this value is also equal to $N \times FTF$. However, you would be wrong.

The mistake is in the fact that in this case, the inner race is also rotating. Previously, we were able to directly use the $FTF$ since the outer race is not moving, so we only had to worry about the rotation of the rollers around the bearing. In this case, however, both the inner race and the rollers are moving, so we have to consider the effect of both rotations.

One way to think about this is to try to consider the problem in a frame of reference where the inner race is stationary instead. To keep the inner race stationary, we have to rotate our frame of reference by an angular frequency of $S$, to “undo” the rotation of the inner race. When we do this though, we would also observe the roller to be revolving with a new angular frequency. In the original frame, the angular frequency of the roller is the $FTF$. In the new frame, the roller would be revolving with an angular frequency of $FTF - S$.

Similarly, since we have $N$ rollers, the frequency will go up by $N$ times from the same reason as earlier. This means that

Note about this one:

• We have used absolute value since there is a chance $FTF - S$ is negative.
• I haven’t shown you that we can add or subtract angular frequency when we shift frames of reference. I’ll leave that part as an exercise for the reader to ponder on. I couldn’t think of a better way to derive the $BPFI$ so got to do it this way for now :/.

Ball Spin Frequency (BSF)

This is the rate where a point on the roller comes into contact with one of the races. We can imagine having a mark where the roller touches the inner or outer race, and the $BSF$ corresponds to how frequently that point touches either race while it is revolving around the bearing. You can try to convince yourself that it doesn’t matter whether you consider the outer race or the inner race.

Because we have this choice of race, we can choose the outer race as it is more convenient to think about (since the inner race is moving and we would require shifting of frames like how we have done to calculate the $BPFI$). I’ll leave this part as an exercise for the readers.

We know that the frequency of the revolution of the roller around the outer race is $BPFO$. During one revolution of the roller around the outer race, we see that the roller will rotate around itself $\frac{P_o}{R}$ times. This is because one revolution around the outer race will mean the roller has rolled a distance of $2\pi P_o$ (circumference of outer race), and for one rotation around itself the roller needs to travel a distance of $2 \pi R$ (assuming no slipping).

This means that during one revolution around the outer race, a point on the roller would have contacted the outer race $\frac{P_o}{R}$ times. If the roller revolves around the outer race with a frequency of $BPFO$, then a point on the roller will come in contact with the outer race with a frequency of

Restating The Equations A Bit

Some of the expressions above look a bit messy, so let’s clean it up.

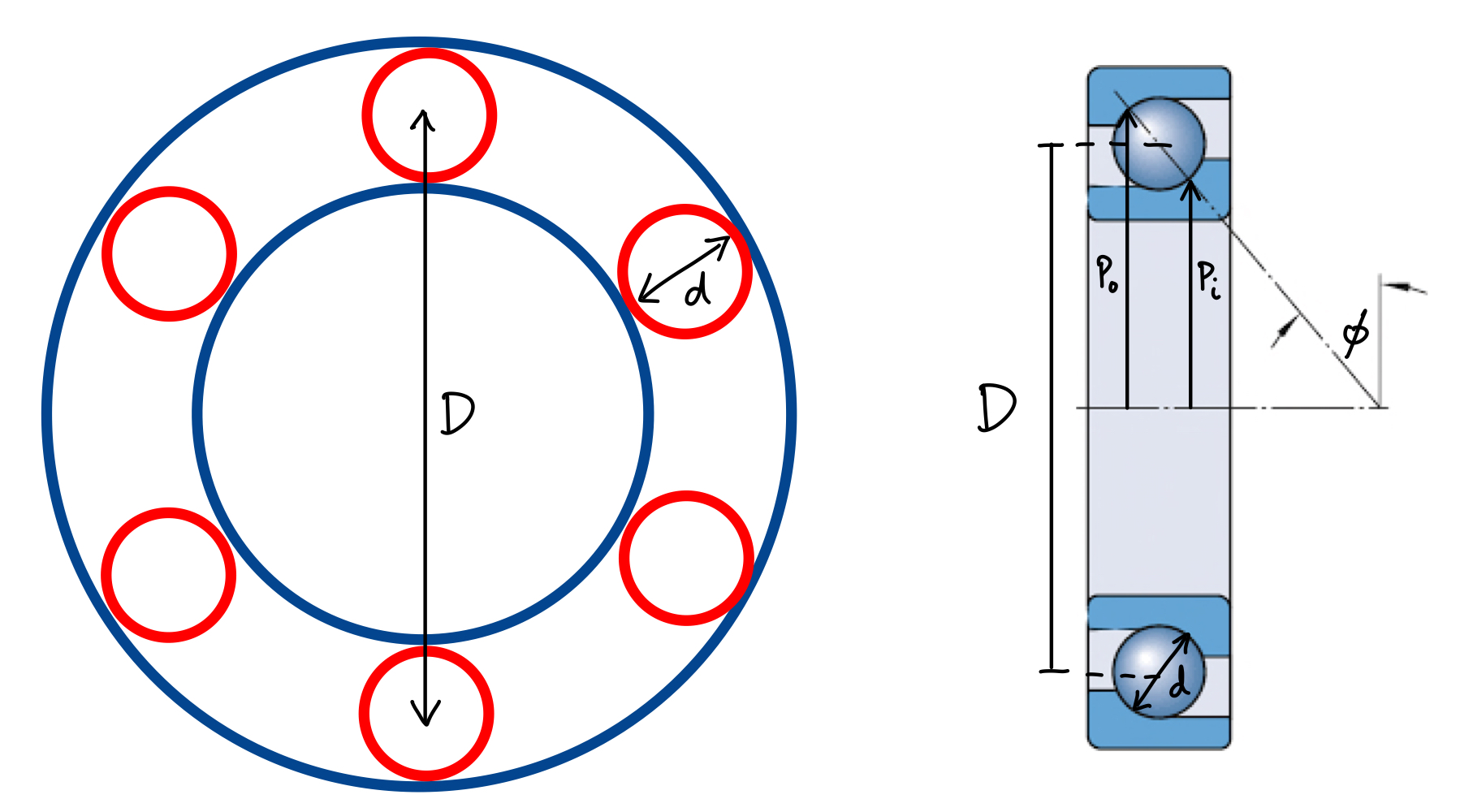
Cross-section of a bearing (right image taken from here)

In most cases we only know the diameters of the roller and the diameter of the cage. Suppose we let $D$ be the diameter of the cage and $d$ be the diameter of the rollers. Then, $D = 2P$ and $d = 2R$.

Bearings will usually have some is the contact angle $\phi$, which is the angle that the races touch the roller. Given this geometry (and the diagram on the right), it is easy to convince yourself that the $2P_i = D - d\cos \phi$ and $2P_o = D + d\cos \phi$.

Substituting these values in, we finally find the roller frequencies to be as follows: